Worksheets to Whiteboards: Rethinking the Math Classroom

Not too long ago, my math block started the same way every day: students walked in, grabbed their notebooks, and started a warm-up. Some finished quickly. Others struggled. A few zoned out. And me? I was already at the back table trying to reteach yesterday’s concept to a small group. It was routine. Predictable. Quiet. But deep down, I had to admit—it wasn’t working. I knew my students were capable of more. I just didn’t know how to get them there.

In Building Thinking Classrooms in Mathematics K-12, Peter Liljedahl invites us to rethink what our math classrooms could look like by using simple but powerful tools that shift our students from passive participants to active thinkers. Let’s get started rethinking the math classroom!

No Magic – Small Moves That Work

I’ll let you in on a little secret: there’s no one “perfect” activity that guarantees engagement and collaboration. But if you’re here looking for ways to build a math classroom where thinking really happens, stick with me. In Building Thinking Classrooms in Mathematics K-12, Liljedahl shares findings from 15+ years of research into what actually gets students thinking. He studied 14 different teaching variables and distilled them into 14 optimal practices you can implement right away.

In this article, we’re diving into the first Toolkit from the book. It includes three big moves:

• Giving Rich Thinking Tasks
• Frequently Forming Visible Random Groups
• Using Vertical Non-Permanent Surfaces (VNPSs)

Start With a Rich Thinking Task

Liljedahl’s top advice for getting started? Use non-curricular tasks first. These aren’t about standards or test prep. They’re about building the muscles of problem-solving (getting stuck, experimenting, failing, trying again) and learning through the process.

“Good problem-solving tasks require students to get stuck and then to think.”

Peter Liljedahl

Letting students struggle through a math problem is one of the most powerful things a teacher can do to support deep learning. It might feel counterintuitive at first. After all, teachers are helpers by nature. But here’s the thing: struggle isn’t a sign of failure. It’s a sign that thinking is happening.

Think of it like this: When there’s a road closure, we don’t just sit there—we find a new route. That is what we want students to do with math problems. If we’re always jumping in to “rescue” them, they’ll never learn how to reroute on their own.

What Makes a Good Problem-Solving Task?

According to the National Council of Teachers of Mathematics (NCTM), quality math tasks should:

• Embed important, useful mathematics.
• Require higher-level thinking and problem-solving.
• Contribute to conceptual development.
• Allow for teacher assessment and feedback.
• Support multiple solution strategies.
• Encourage engagement and discourse.
• Connect to other mathematical ideas.
• Promote skillful use of mathematics.

Liljedahl says it best, “What makes a good problem-solving task is not what it is, but what it does. What they do is make students think.”

Problem-Solving Tasks

To reach all learners and rethink the math classroom, we need low-floor, high-ceiling tasks. These tasks are easy to enter but offer room for challenge. Early success with a task motivates and empowers students to persevere through the struggle. 

One key feature of an effective thinking task is novelty. It needs to be something students haven’t encountered before. When a task feels new, students can’t rely on memorized steps or mimicry. Instead, they’re pushed to truly think, explore, and reason their way through it.

Extensions are essential to keep the thinking going. These layered challenges allow the task to evolve, offering all students a chance to engage in incremental struggle. As the task progresses, learners meet just the right amount of challenge at just the right time.

Productive Struggle

This sweet spot is what we call productive struggle. Productive struggle is a state of effortful learning where students work through problems that stretch their thinking. It’s in this space that they build grit, sharpen problem-solving skills, and develop a deeper, more meaningful understanding of the concepts at hand.

At a Building Thinking Classroom (BTC) conference in 2024, Liljedahl shared a brilliant analogy:

“We have to pick tasks that students can be successful at to begin with. We’ve got to back the train up as far into the station as necessary for all of the students to get on the train. Then, the train leaves the station, and now the teacher’s job is to keep everyone on the train, which is a lot easier than pulling out of the station with two kids in the snack bar, three in the restroom, and four on the wrong platform. Now two-thirds of the kids are on the train, and one-third of the students are back at the station, going, ‘What happened?’

Now, teachers have a very complex job. If teachers want to pick a task that everyone can participate in, they have to pick a task that one-third of the students will think is too easy.

About a third of the students will look at the teacher like they’ve lost their minds, and this is too simple. If they’ve done that, then everyone is on the train. If the teacher picks a task where the majority of the students think it is too hard, they’ve just left some of their class back at the station. The train is going to move forward, and the task will get harder, but teachers have got to get everyone on the train first.”

Getting Started With Rich Thinking Tasks

Liljedahl offers resources to get teachers started on his website.

Support All Learners with Multiple Representations

Worried about students who get stuck? You’re not alone. That’s where mathematical representations come in.

In Principles to Actions, the National Council of Teachers in Mathematics (NCTM) (2014, p.24) highlights the value of using multiple representations in math learning:

“When students learn to represent, discuss, and make connections among mathematical ideas in multiple forms, they demonstrate deeper mathematical understanding and enhanced problem-solving abilities.”

NCTM

In Thinking Classrooms, students work together to move between different models, such as visual, symbolic, or concrete representations. As they do, they become more fluent in the language of mathematics. This translation process not only deepens understanding but also builds confidence.

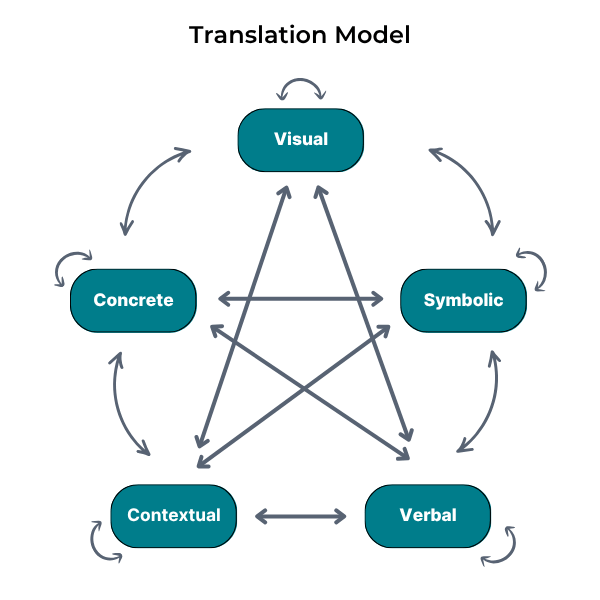
Creating a space where students can experiment with ideas and explain their thinking with the support of different representations is even more powerful when paired with the right tools. This is part of rethinking the math classroom.

In their book, Mathematics Tasks for the Thinking Classroom, Grades K–5, Peter Liljedahl and Maegan Giroux reinforce the importance of providing concrete manipulatives to support students’ problem-solving development. These math tools help all learners make sense of abstract ideas and develop more flexible, connected thinking. This is especially true for our young learners who are developing foundational math vocabulary.

“The manipulatives give the students models to think about, think with, and communicate with while the vertical non-permanent surface provides a workspace that has been proven to create better engagement, enthusiasm, perseverance, knowledge mobility, time on task and thinking.”

Liljedahl and Giroux

3 Ways Manipulatives Support Mathematical Conceptual Understanding

Rethinking the Workspace in a Thinking Classroom

In a Thinking Classroom, the traditional pencil-and-paper routine takes a backseat. Instead, students are on their feet, tackling problems on vertical non-permanent surfaces like whiteboards, chalkboards, windows, or anything that gets them moving, collaborating, and thinking visibly.

These surfaces aren’t just about novelty; they disrupt old patterns of disengagement and promote active learning. With only one marker per group, students must verbalize their ideas to the annotator and explain their reasoning as they problem-solve together.

Liljedahl’s research found that when students work on non-permanent surfaces, the following happens:

• Thinking starts faster. Students begin problem-solving within 20-30 seconds compared to several minutes at a desk.
• Engagement increases. There’s something about standing up that signals the brain, “It’s go time.”
• Mistakes are embraced. A dry-erase marker feels less permanent than ink, reducing the fear of failure.

Visibility changes everything. When students are seated at their desks, they often feel invisible. They are less likely to speak up, share ideas, or take risks. This setup reflects the post-industrial model of education, designed more for compliance and efficiency than creativity and collaboration. It mirrors a time when schools prepared students for factory work, not for thinking critically.

Working on Vertical Non-Permanent Surfaces

In contrast, when students are working on vertical non-permanent surfaces (VNPS), the dynamic shifts. Teachers can instantly see where each group is in their thinking. Who’s stuck, who’s soaring, and who may need a nudge in the right direction. And the students? They can glance around the room, check out other boards, and draw inspiration from their peers. This sparks conversation and idea-sharing.

This visibility isn’t just logistical but transformational.

Research Supports VNPS

After 15 years of research, Liljedahl determined that, “Students working at VNPSs spent more time engaged in active thinking than when seated at desks.”

When it comes to our youngest learners, especially those in Grades K–2, Liljedahl points out an important distinction. These students haven’t yet been “encultured” to disengage at their desks. Because of that, it’s perfectly effective for them to use horizontal non-permanent surfaces, whether at their seats or spread out around the classroom. The key is keeping the work erasable and the thinking visible, regardless of the angle.

Shuffling Groups for Success

Group work is not new. But how groups are formed makes all the difference. Liljedahl suggests teachers remove themselves and their students from the “nexus of control” by creating visibly random groups of two to three students every day.

That means drawing names, picking from a deck of cards, rolling dice–anything that students see as random. No teacher picks. No friend cliques. Just pure chance.

For younger students, Liljedahl recommends groups of two. “Students at this age are still developmentally in a stage of parallel play, and collaboration consists mostly of polite turn-taking.” Switching these groups randomly and visibly, after every transition, is one of his strongest recommendations for students in Grades K–2.

Benefits of Random Grouping

Liljedahl recognized a few benefits throughout his research on forming visibly random groupings:

• Reduced social status. When groupings change daily, no one dominates or gets left behind.
• Community building. Over time, students learn to work with everyone, not just their inner circle.
• Increased participation. Students are more likely to engage when they can’t predict who they’ll be with, and everyone’s expected to contribute.

Yes, it feels a little awkward at first. However, Liljedahl found that after three weeks of consistent, visibly random grouping, classroom culture began to shift. Students became more comfortable making mistakes, asking questions, and thinking out loud. They’re no longer worried about who they were paired with.

“Students reported feeling more comfortable taking risks and being wrong in these random groupings…they started seeing mistakes as part of the process, not something to avoid.”

Liljedahl

Getting Started With Visibly Random Grouping

From Lecturer to Learning Coach

Let’s be honest—most of us were taught to teach from the front of the room. But BTC invites teachers to shift from professor to facilitator. Liljedahl encourages teachers to make this shift, moving away from the 19th-century classroom to achieve 21st-century goals.

When students are working on meaningful tasks in random groups at vertical surfaces, the teacher is free to observe, question, and support thinking in real time. Hints and extensions support students as they struggle through tasks that challenge them to think about math in a way they have never experienced before. (We will explore hints and extensions to maintain flow in a later blog post.)

Teachers stop being the “answer key” and start being a thinking coach.

Letting students struggle doesn’t mean leaving them floundering. It means giving them just enough support to keep going. This might look like:

• Asking a probing question instead of giving an answer.
• Encouraging students to try a different strategy.
• Redirecting students to talk to a peer.
• Simply saying, “Keep going, you’re on the right track.”

Final Thought on Rethinking the Math Classroom: It’s Okay if It’s a Little Messy

You don’t avoid hallway walks just because your students don’t form a perfect straight line, right? The same goes for thinking.

Students need to experience doing the work of problem-solving—even if it’s a little bumpy. Give them the tools, give them the task, and let them explore.

Start small. Try a low-floor, high-ceiling thinking task. Draw names for random groups. Organize non-permanent spaces. You don’t have to change everything overnight. Every little shift moves you closer to a classroom where thinking thrives.

Trust me, once you see the spark in your students’ eyes when they realize they are doing the math, you won’t want to go back.

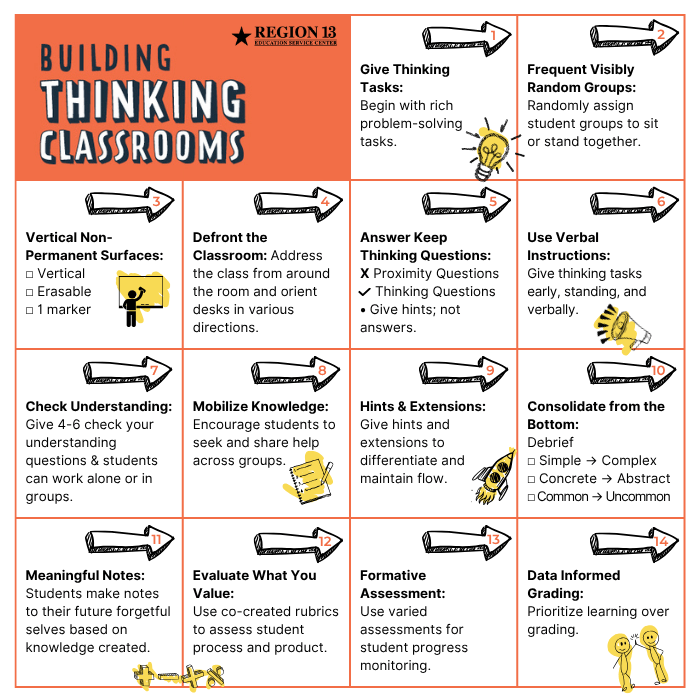
Conclusion

Follow our blog series to keep digging into the 14 optimal practices you can put in place to transform your math classroom! Missed one of our other math articles? Find them on the ESC Region 13 blog here.

Keep up with the latest in math news and updates by subscribing to our newsletter. And don’t forget to check out the current math workshops to continue your professional development.

Let’s keep the conversation going. Have you tried rich tasks, used non-permanent surfaces, or frequently visibly random groups in your classroom? What surprised you? What challenges did you face? Drop a comment below, I’d love to hear from you! Have a question? Don’t hesitate to reach out at alejandra.gonzalez@esc13.txed.net.

References:

Liljedahl, P. (2021). Building Thinking Classrooms in Mathematics Grades K-12. Corwin.

National Council of Teachers of Mathematics. (2014). Principles to Actions: Ensuring Mathematical Success for All. NCTM.

Liljedahl, P., & Giroux, M. (2023). Mathematics Tasks for the Thinking Classroom, Grades K–5. Corwin.