What is Mathematical Proficiency?
How do you define mathematical proficiency? Had I been asked this question early in my teaching career, I might have defined it as the ability to solve problems efficiently and accurately. In the back of my mind, I might have thought it meant having good number sense for procedural computations or equation solving. The five strands of Mathematical Proficiency are conceptual knowledge, procedural fluency, strategic competence, adaptive reasoning, and productive disposition.
Honestly, as a student, I was really good at memorizing and following procedures. I excelled in math the way I was taught. Through lectures and endless procedural practice. Therefore, my personal math experiences informed my definition of mathematical proficiency and my initial instructional style. Luckily, I do love to learn! As a novice teacher, I read several articles and books and attended professional learning opportunities over the years. These outlets enhanced my view, definition, and understanding of mathematical proficiency.
What it Means to Learn Math Successfully
To be proficient in mathematics means that one learned mathematics successfully. But what is the threshold for that success? What skills does a student possess and demonstrate that deems them mathematically proficient? I pursued professional learning opportunities seeking answers to these questions.
One impactful professional learning workshop I attended shared some research from the National Research Council. At the end of 1998, the National Research Council established the Committee on Mathematics Learning including a diverse group of math education experts from across the country.
These experts were tasked to:
- Synthesize the rich and diverse research on mathematics learning.
- Provide research-based recommendations for teaching, teacher education, and curriculum for improving student learning.
- Identify areas where research is needed.
- Give advice and guidance to educators, researchers, publishers, policymakers, and parents.
In 2001, the National Research Council published Adding It Up: Helping Children Learn Mathematics, which details the committee’s report. Many people reference this report often using the committee’s definition of mathematical proficiency. Their definition explains what it means for anyone to learn mathematics successfully.
Conceptual Knowledge and Procedural Fluency
The report states that mathematical proficiency has multiple interwoven and interdependent strands.
Two specific strands that our math community discusses often are conceptual knowledge and procedural fluency.
- Conceptual Knowledge – the comprehension of mathematical concepts, operations, and relations
- Procedural Fluency – the skill of carrying out procedures flexibly, accurately, efficiently, and appropriately
Procedural Fluency
The National Council of Teachers of Mathematics (NCTM) references the Committee on Mathematics Learning definition of procedural fluency, as does our own K-5 Texas Essential Knowledge and Skills (TEKS) Math Standards.
Introductory paragraph three of the K-5 Math TEKS states:
“For students to become fluent in mathematics, students must develop a robust sense of number. The National Research Council’s report, “‘Adding It Up,”’ defines procedural fluency as ‘skill in carrying out procedures flexibly, accurately, efficiently, and appropriately.’ As students develop procedural fluency, they must also realize that true problem solving may take time, effort, and perseverance.”
K-5 Math Texas Essential Knowledge and Skills
Through House Bill 4545, the 87th Legislature implemented the Strong Foundations Grant Program (Texas Education Code, 29.0881) in 2021. The program offers K–5 Math comprehensive Tier 1 instructional supports, including curriculum, instructional leadership, and planning supports.
The grant resulted in the creation of Research-Based Instructional Strategies (RBIS). Now Texas math classrooms incorporate RBIS, a set of practices supported by research, regardless of instructional materials. The RBIS are based on the science of how students best learn math in K-12 classrooms.
RBIS 1 is the balance of conceptual with procedural. This means we should pursue rigor by balancing conceptual understanding, procedural skill, and fluency, and apply this balanced understanding to mathematical applications as required by the standards in the TEKS.
Conceptual knowledge and procedural fluency are only two of the strands of mathematical proficiency. In order to promote mathematical proficiency in students, these two strands are only the beginning of what we should develop in our students and seek out in our instructional resources.
Other Strands of Mathematical Proficiency
The remaining three strands of mathematical proficiency are:
- Strategic Competence – the ability to formulate, represent, and solve mathematical problems
- Adaptive Reasoning – the capacity for logical thought, reflection, explanation, and justification
- Productive Disposition – the habitual inclination to see mathematics as sensible, useful, and worthwhile, coupled with a belief in diligence and one’s own efficacy
The numbering of the strands does not constitute a specific sequence or weight of importance.
As previously stated, all strands are interwoven and interdependent. The strands create a woven braid of mathematical proficiency that is strong yet flexible.
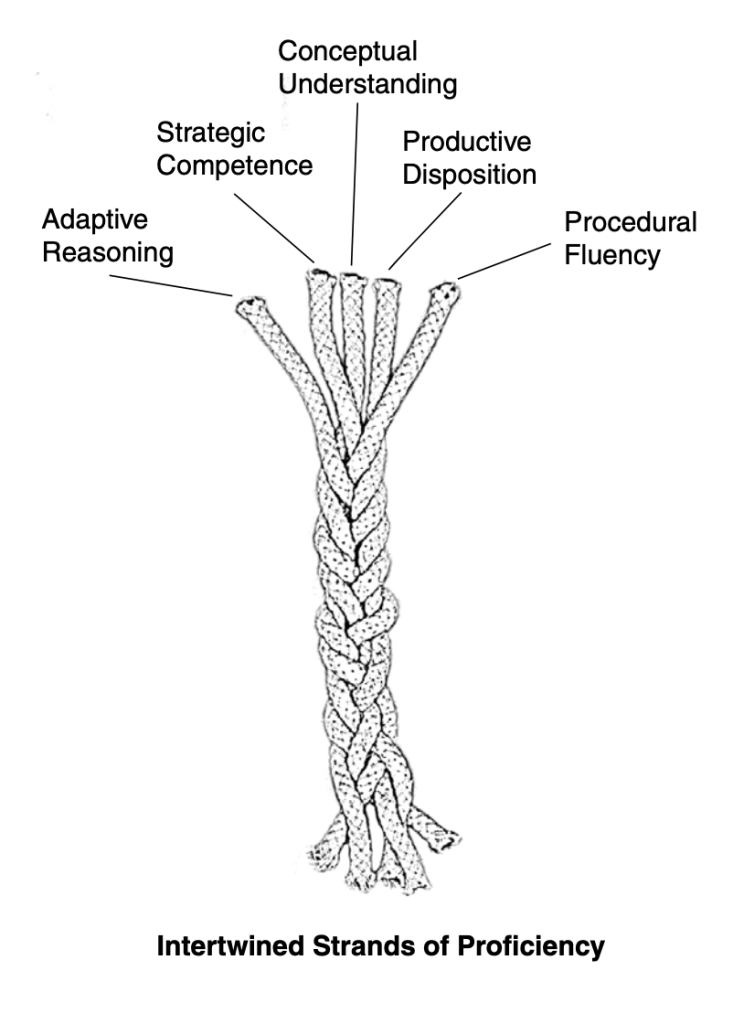
When viewing all strands of mathematical proficiency, it seems obvious that they are important for teaching and learning mathematics.
For instance, look at our own K-12 TEKS Mathematical Process Standards for alignment to the strands of mathematical proficiency. Where do you see evidence of the strands in the process standards?
Mathematical Process Standards
(1 ) Mathematical process standards. The student uses mathematical processes to acquire and demonstrate mathematical understanding. The student is expected to:
Mathematical Process Standards
(A) apply mathematics to problems arising in everyday life, society, and the workplace;
(B) use a problem-solving model that incorporates analyzing given information, formulating a plan or strategy, determining a solution, justifying the solution, and evaluating the problem-solving process and the reasonableness of the solution;
(C) select tools, including real objects, manipulatives, paper and pencil, and technology as appropriate, and techniques, including mental math, estimation, and number sense as appropriate, to solve problems;
(D) communicate mathematical ideas, reasoning, and their implications using multiple representations, including symbols, diagrams, graphs, and language as appropriate;
(E) create and use representations to organize, record, and communicate mathematical ideas;
(F) analyze mathematical relationships to connect and communicate mathematical ideas; and
(G) display, explain, and justify mathematical ideas and arguments using precise mathematical language in written or oral communication.
I would argue that if we are truly planning our lessons to provide intentional opportunities for students to develop and demonstrate the TEKS Mathematical Process Standards, then we are focusing on developing mathematically proficient students.
Take Time to Reflect
Take some time to reflect on your own glows and grows when it comes to creating opportunities in your classroom that promote mathematical proficiency.

In support of your own reflection, I will be vulnerable and share that in my first few years as a classroom teacher, I struggled with the strand of productive disposition. I taught multiple sections of “Repeater Algebra I” and struggled with the fact that students always asked, “When am I ever going to use this?” or stated, “I have never been good at math and never will be, so why try?”
Such statements highlight the fact that these students did not have a productive disposition for mathematics. Many of my students didn’t see the relevance of the math they were learning in their classroom to their everyday lives. They didn’t view math as useful or sensible, and they lacked self-efficacy for math due to their negative past experiences.
After much reflection, I realized the instructional resources I was using, and the experiences I had been creating in my classroom were not focused on developing my students’ productive disposition for mathematics. Therefore, I had to do something different and do it right away because my students deserved better.
Growth vs. Fixed Mindset
I began to research what I could about developing a productive disposition, and that is when I was introduced to the concept of growth vs. fixed mindset. I read early articles from Dr. Carol Dweck, who defined mindset and its impact on learning. She later detailed this research in her book Mindset: The New Psychology of Success.
The diagram below is by Nigel Homes. It represents growth vs. fixed mindset as shown in Dr. Carol Dweck’s book. It is used to help define her work.
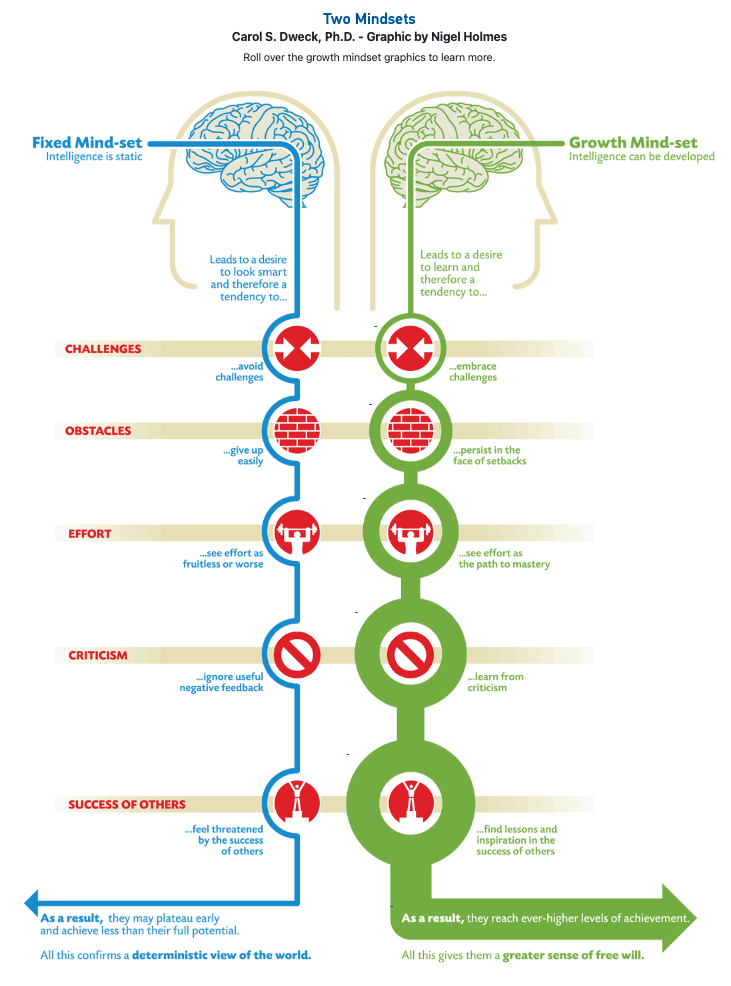
My students who stated they were never good at math held a fixed mindset. Their previous negative experiences in math made them view their failure in math as part of their identity. Therefore, these students did not believe that they could ever be successful in mathematics. This belief impacted their ability to try, to care, or to learn. I knew I needed to foster a growth mindset environment in my classroom that supported the belief that effort creates ability.
In the growth mindset environment, if a student doesn’t succeed on an assignment or assessment, they view it as an opportunity for growth rather than a failure. Failure does not define their identity. They are just not successful yet and there is an opportunity to still learn with success. This self-efficacy is foundational for a productive disposition.
Learning Math with Understanding
While doing my research into productive disposition, I found a book by James Hieber, et al. titled Making Sense: Teaching and Learning Mathematics with Understanding. The authors stress the importance of students learning math with understanding. They state, “Understanding is crucial because things learned with understanding can be used flexibly, adapted to new situations, and used to learn new things. Things learned with understanding are the most useful things to know in a changing and unpredictable world.” This made me question how I defined learning with understanding.
The following example from the book helped clarify learning with understanding for me,
“When we memorize rules for moving symbols around on paper we may be learning something, but we are not learning mathematics. When we memorize names and dates we are not learning history; when we memorize titles of books and authors we are not learning literature. Knowing a subject means getting inside it and seeing how things work, how things are related to each other, and why they work like they do.”
This solidified the level of mathematical understanding I would strive to develop in my students.
Teaching and learning math with understanding is also aligned with developing students’ conceptual knowledge, procedural fluency, and using these understandings to solve problems. But for students to demonstrate their understanding, they must utilize their adaptive reasoning skills to explain and justify how they solved their problems and why it makes sense. This supports the claim that all strands of mathematical proficiency are necessary, interwoven, and interdependent.
A Challenge
Who knew that attending that one workshop early in my career and learning about the strands of mathematical proficiency would lead me down this path towards professional growth? I am grateful it led me to do research about improving my teaching practices and seeking professional learning opportunities. But reading and attending professional learning opportunities do not simply change one’s practices and impact student learning. All that knowledge gained had to be put into practice, so I began to challenge myself to implement little by little what I was learning.
Therefore, my hope is that in reading this blog, it might impact a reflection on your own teaching practices and beliefs and begin your journey in professional growth.
My challenge to you is to reflect on the five strands of mathematical proficiency and think about your grow area(s). What can you commit to doing that promotes growth in those specific strands?
For more information on math professional development opportunities at ESC Region 13, visit our website. If you’d like to stay up-to-date on the latest math news, we’d love for you to subscribe to our monthly newsletter.
References:
Dweck, Carol S. 2006. Mindset: The New Psychology of Success. New York: Random House Publishing Group.
Hiebert, James, Thomas P. Carpenter, Elizabeth Fennema, Karen C. Fuson, Diana Wearne, Hanlie Murray, Alwyn Olivier, and Piet Human. 1997. Making Sense: Teaching and Learning Mathematics with Understanding. Portsmouth, NH: Heinemann.
National Research Council. 2001. Adding It Up: Helping Children Learn Mathematics. Washington, DC: The National Academies Press. https://doi.org/10.17226/9822.
TEA Strong Foundations https://sites.google.com/tea.texas.gov/sfp/navigation/research-based-instructional-strategies)
Sami Briceño
Sami Briceño is the Secondary Math Specialist at Education Service Center Region 13.




Add comment